Orbital Mechanics (Advanced). Kepler's laws
Johannes Kepler's laws of planetary motion describe the movement of planets around the Sun more accurrately than previous models, improving the Heliocentric model proposed by Nicolaus Copernicus. The most notable diference between these models is that orbits are not perfect circles, but ellipses (a circle is a special case of an ellipse).
Kepler's first law
The first law states that 'The orbit of a planet is an ellipse with the Sun at one of the two foci.'
A focus is a point with reference to which an ellipse is drawn. The further they are from each other, the wider the ellipse. An ellipse whose foci are at the same point is a circle. An illustration can be seen below showing the major points and sections in an ellipse.
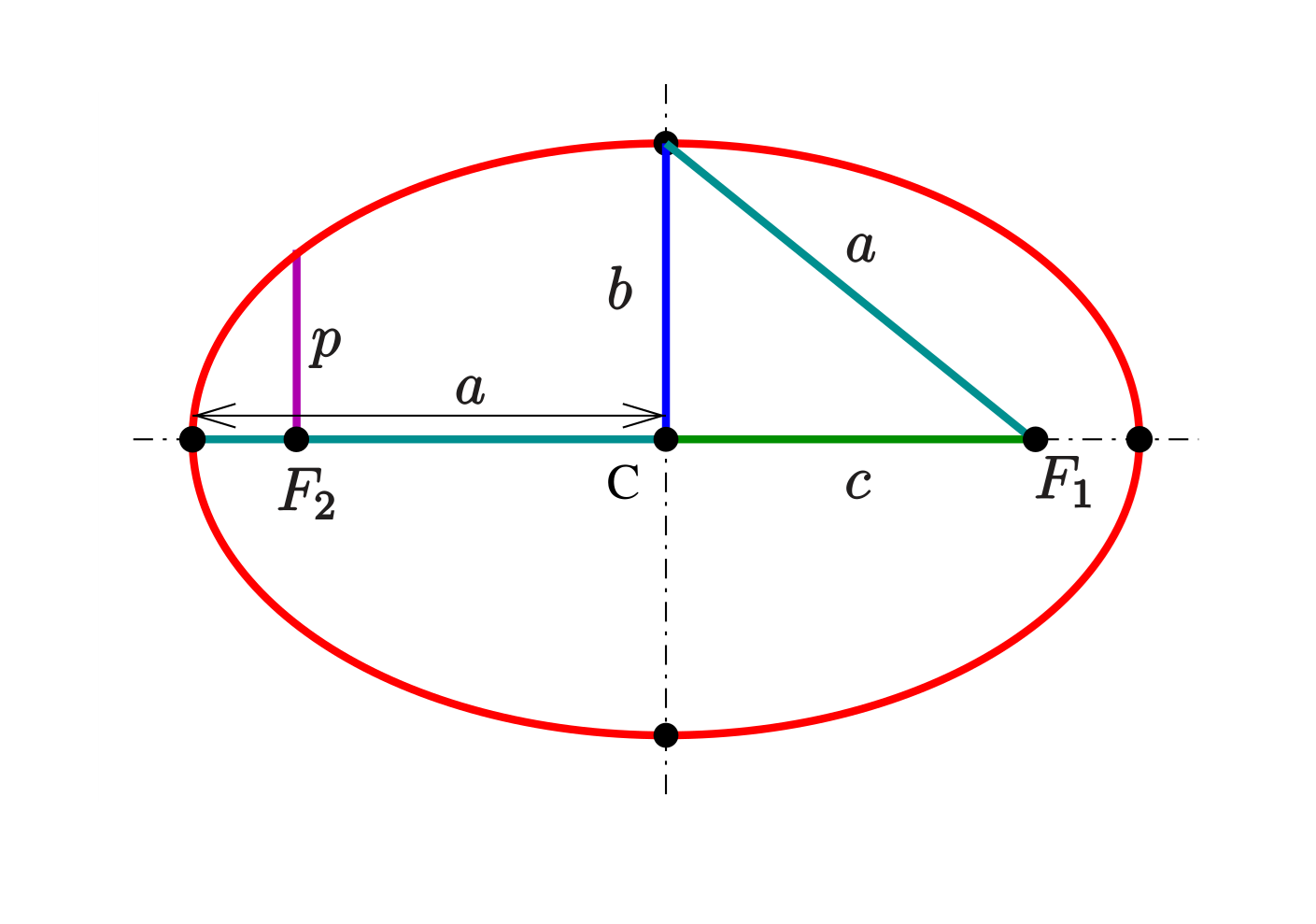
Illustration by Ag2gaeh, CC BY-SA 4.0
'a' is the semi-major axis- the longest radius of the ellipse, extending from the center to the edge along the major axis.
'b' is the semi-minor axis- the shortest radius of the ellipse, extending from the center to the edge along the minor axis.
'c' is the distance from the center of the ellipse to one of the foci.
'p' is the semi-latus rectum- the distance from a focus to the ellipse along a line perpendicular to the major axis.
F1 and F2 are the foci of the ellipse.
Eccentricity is a measure of how wide an ellipse is. It is defined by: e = c a.
A few formulae can be used to find out the parameters of the orbit (the ellipse):
x2 a2 + y2 b2 = 1, where the center is at (x,y)=(0,0). This is the mathematical definition of an ellipse.
p = a(1 - e2);
Q = a(1 + e), where Q is the largest distance from the ellipse to a focus (the apoapsis distance of the body from the body it orbits).
q = a(1 - e), where q is the smallest distance from the ellipse to a focus (the periapsis distance of the body from the body it orbits).
c2 = a2 - b2;
r = p 1 + e cos θ, where r is the distance between the two objects (for example, a planet and a star), and θ is the angle the orbiting body has moved from periapsis.
v2 = G(M+m)( 2 r - 1 a), where v is the orbital speed, G is the gravitational constant, M and m are the masses of the two objects in a system, r is the distance between these bodies, and a is the semi-major axis. This is the vis-viva equation.
Kepler's second law
The second law states that 'A line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time.'
This means that for any given time period, the area that will be touched by the imaginary line connecting the planet and the star is going to be constant, given that the time period stays constant.
The entire area of an ellipse is A = π·a·b.
As seen in the picture below, the two equal areas, coloured in light gray and dark gray, take the same time for the planet to cross.
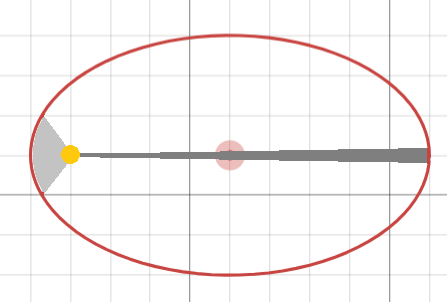
The areas are not to scale. The red circle is the center, and the yellow circle is the star a planet orbits.
Kepler's third law
The third law states that 'The square of a planet's orbital period is proportional to the cube of the length of the semi-major axis of its orbit.'
In different terms, T2 a3 = const.,
where T is the period of the planet's orbit, and a is the length of the semi-major axis.
This can be derived for a circular orbit:
Fc = Fg
mv2 r = GMm r2
v2 = GM r
Considering that r = a in a circular orbit;
S2 T2 = GM a (2πa)2 T2 = GM a a3 T2 = GM 4π2 T2 a3 = 4π2 GMTherefore, for all bodies orbiting the same star in an approximate two-body system (where the main source of gravity is the star), T2 divided by a3 is constant, as the only variable on the right side of the equation, M, is constant too.
Practice Question
A planet is orbiting a star on a coordinate plane. Find the period of the orbit in years, if the planet crossed points A(10,4) and B(14,3), where the units are AU; 1 AU = 1.496·1011 m. The ellipse is centered at (0,0), and the mass of the star is 1.989·1030 kg, G = 6.674×10-11 m3⋅kg-1⋅s-2. Consider that a year is 365 24-hour days.